Proyecto Patrimonio - 2014 | index | María-Elvira Luna-Escudero-Alie | Autores |

Variable aleatoria discreta o «la aberración de las matemáticas» en “Tigres azules”
y los límites del lenguaje en “El espejo y la máscara” de Jorge Luis Borges
Stephen Kcenich, MS, Montgomery College, MD
María-Elvira Luna-Escudero-Alie, PhD., MC, MD
Proyecto_borges@yahoo.com
A Lee y Bill Kcenich
.. .. .. .. .. .
El tiempo es la sustancia de que estoy hecho. El tiempo es un río
que me arrebata, pero yo soy ese río; es un tigre que me destroza,
pero yo soy el tigre; es un fuego que me consume, pero yo
soy el fuego. El mundo, desgraciadamente, es real; yo,
desgraciadamente, soy Borges (O.I. 256)
El complejo mundo borgeano pleno de panteísmo, laberintos, espejos, sueños, digresiones sobre el infinito, reflexiones sobre la caótica realidad, el tiempo y el espacio, nos impele insistentemente a analizar, entre otras consideraciones, los múltiples conceptos metafísicos inmersos en sus exquisitos textos. En este artículo en particular, hemos reflexionado sobre dos cuentos: “Tigres azules”, y “El espejo y la máscara”. Nuestra reflexión sobre “Tigres azules” se ha servido de conceptos prestados de la estadística y la teoría de probabilidades, específicamente hemos aplicado la variable aleatoria discreta en un intento por encontrar un patrón a una realidad numérica cambiante cuya variación parece gobernada por el caos. En cuanto al relato: “El espejo y la máscara”, hemos relexionado sobre los límites del lenguaje que, a nuestro parecer, dicho relato propone. Hemos hecho también un análisis contrastivo profundizando en la analogía que encontramos entre los límites del lenguaje; postulado del cuento “El espejo y la máscara”, y la restricción de las matemáticas para explicar un fenómeno cuantitativo, que también vemos como un postulado de “Tigres azules”.
Empecemos por resumir el argumento de ambos cuentos y luego de comentar cada relato, reflexionaremos sobre el puente metafísico que, en nuestra opinión, los conecta indefectiblemente.
El relato “Tigres azules”, el segundo de los cuentos incluidos en el último libro de relatos de Borges titulado: La memoria de Shakespeare (1983), tiene como protagonista a Alexandre Craigie; un profesor escosés de lógica occidental de la Universidad de Lahore, que los domingos se dedica a estudiar la obra del filósofo holandés Baruch Spinoza. El profesor Craigie estaba obsesionado desde niño con tigres (al igual que el propio Borges lo estuviera), y supo a fines de 1904 que en la región del delta del Ganges había sido descubierta una variedad azul de tigres. Craigie aprovechó sus vacaciones para viajar a la India, al Punjab.
Alexandre Craigie no encontró en el Punjab tigres azules sino historias y sagas populares sobre su supuesta presencia. Incluso tuvo la impresión de que los aldeanos veneraban como divinidad al tigre azul. A falta de tigres azules, el profesor Craigie halló unas extrañas pequeñas piedrecitas lisas, circulares y de un azul brillante, como el del tigre de sus sueños. El profesor Craigie observó que estas piedrecitas azules que semejaban pequeños discos o fichas se multiplicaban o disminuían indiscriminadamente. El misterioso fenómeno, esa “aberración de las matemáticas”, producido por “las piedras que generan”, apodadas por los aldeanos “tigres azules”, intrigó al profesor de lógica occidental. El profesor constató, no obstante su formación académica, que en el universo cabía el desorden, y también la carencia de lógica. Trató de entender la variación numérica de las piedras usando la estadística, después de haber fracasado con las cuatro operaciones básicas de la aritmética, y también con el cálculo de probabilidades. El 10 de febrero, Alexander Craigie entró a la mezquita Wazil Khan a la hora “en que la luz no ha revelado los colores”, y rezó para ser eximido de “su carga”. Súbitamente se le apareció un mendigo ciego, y le pidió limosna. El profesor Craigie le dijo que no tenía monedas, y el ciego respondió que por el contrario, tenía muchas. Cuando Alexandre Craigie le entregó las piedras azules, el mendigo le dijo: “Te quedas con los días y las noches, con la cordura, con los hábitos, con el mundo”. Y luego el mendigo ciego desapareció en el alba tan misteriosamente como había aparecido.
El relato “El espejo y la máscara”, el séptimo de los cuentos incluidos en la penúltima colección de cuentos de Borges, El libro de arena (1975), nos narra una fábula cuyas acciones ocurrieron en Irlanda, durante la primera época de la Edad Media. Los hechos narrados sucedieron en el marco temporal inmediatamente posterior a la batalla de Clontarf. El “Alto Rey” irlandés le propone al poeta de su corte que inmortalice la victoria sobre los noruegos en una oda. Después de un año “el Ollán” recita de memoria su oda y se la entrega al rey quien la acepta y premia su esfuerzo con un espejo de plata. El rey le dice al poeta que su poema será copiado sesenta veces por los escribas de su Corte y que de su pluma maestra espera un poema aun mejor:
“[…] Acepto tu labor. Es otra victoria. Has atribuido a cada vocablo su genuina acepción y a cada nombre sustantivo el epíteto que le dieron los primeros poetas. No hay en toda la loa una sola imagen que no hayan usado los clásicos. La guerra es el hermoso tejido de hombres y el agua de la espada es la sangre. El mar tiene su dios y las nubes predicen el porvenir. Has manejado con destreza la rima, la aliteración, la asonancia, las cantidades, los artificios de la docta retórica, la sabia alteración de los metros. Si se perdiera toda la literatura de Irlanda -omen absit- podría reconstruirse sin pérdida con tu clásica oda. Treinta escribas la van a transcribir dos veces.
Hubo un silencio y prosiguió.
-Todo está bien y sin embargo nada ha pasado. En los pulsos no corre más a prisa la sangre. Las manos no han buscado los arcos. Nadie ha palidecido. Nadie profirió un grito de batalla, nadie opuso el pecho a los vikings. Dentro del término de un año aplaudiremos otra loa, poeta. Como signo de nuestra aprobación, toma este espejo que es de plata […]”.
Transcurrido el siguiente año, el poeta regresó con un poema menos largo el cual leyó con inseguridad,
“[…] La página era extraña. No era una descripción de la batalla, era la batalla. En su desorden bélico se agitaban el Dios que es Tres y es Uno, los númenes paganos de Irlanda y los que guerrearían, centenares de años después, en el principio de la Edad Mayor. La forma no era menos curiosa. Un sustantivo singular podía regir un verbo plural. Las preposiciones eran ajenas a las normas comunes. La aspereza alternaba con la dulzura. Las metáforas eran arbitrarias o así lo parecían. […]”.
El rey felicitó al poeta y ordenó que se copiara una sola vez el nuevo poema y que se guardara en un cofre. Como premio por su obra, el rey le ofreció una máscara de oro, y le dijo que de su talento aun esperaba un poema mejor.
El Ollán regresó nuevamente al palacio al cabo de un año. El rey notó el cambio físico del poeta; estaba visiblemente deshecho y tan abatido que sus ojos parecían “mirar muy lejos o haber quedado ciegos”. El poeta no llevaba ningún manuscrito consigo y no se atrevía a recitar el poema. Finalmente lo hizo; era una sola línea oída solamente por el rey. Intrigado por el breve poema, el rey le preguntó al poeta:
“[…] ¿Qué hechicería te lo dio?
-En el alba -dijo el poeta- me recordé diciendo unas palabras que al principio no comprendí. Esas palabras son un poema. Sentí que había cometido un pecado, quizá el que no perdona el Espíritu.
-El que ahora compartimos los dos -el Rey musitó-. El de haber conocido la Belleza, que es un don vedado a los hombres. Ahora nos toca expiarlo. Te di un espejo y una máscara de oro; he aquí el tercer regalo que será el último.
Le puso en la diestra una daga. Del poeta sabemos que se dio muerte al salir del palacio; del Rey, que es un mendigo que recorre los caminos de Irlanda, que fue su reino, y que no ha repetido nunca el poema”.
El estudioso Esteban Mata publicó en la Revista Filosofía, de la Universidad de Costa Rica un ensayo muy lúcido analizando el cuento “Tigres azules” desde la perspectiva de la teoría del caos.
“[…] Por tanto y para concluir, creo que “Tigres azules” puede leerse como una bella parábola que simboliza el advenir del cosmos a partir del caos, una bella imagen de lo indiscernible e indescifrable que es la totalidad, incluso para nuestros más osados y ambiciosos pensamientos.”
Aunque valoramos mucho el análisis de Esteban Mata, nuestra aproximación al relato más bien se centra en la aplicación de conceptos estadísticos tales como la variable aleatoria discreta para descifrar, o al menos, intentar descrifrar los misterios o fenómenos numéricos que ocurren con las piedras azules. Postulamos que sería posible, haciendo algunos cambios mínimos en el relato, hallar un patrón matemático a la metamorfosis numérica que sucede con estas piedras de fábula. Si no hubiéramos hecho las variaciones que hemos realizado al cuento, tampoco habríamos podido encontrar ningún patrón matemático. Alguien podría objetar, acaso el mismo Borges, nuestros cambios aduciendo que ya no se trataría del mismo relato. Y sin embargo hemos hecho estos cambios porque nuestra intención principal es que nuestros estudiantes comprendan la aplicación en la vida diaria de las estadísticas, y que además se beneficien con lecturas literarias que de hecho ampliarán sus horizontes de mundo. Hemos creado un colectivo de aprendizaje (“Learning Community”), que consiste en la unión de dos cursos a través de un tema. Nuestro tema es Borges, en concreto los textos borgeanos donde abundan contenidos matemáticos y para nuestro proyecto académico hemos unido un curso de matemáticas con uno de castellano.
En concreto nos vamos a referir ahora a ejemplos que aplicaremos en nuestro colectivo de aprendizaje, que sólo son posibles, si realizamos unas breves variaciones al cuento de Borges, tal como lo hemos comentado. Por ejemplo, si realizamos un experimento aleatorio con cantidades inciertas, tal como ocurre, con las piedras pequeñas circulares del relato “Tigres azules”, tendremos variables inciertas y sujetas a las muchas posibilidades de la contingencia. Estas cantidades inciertas son las que llamamos variables aleatorias o variables estocásticas. En términos generales, una variable aleatoria, es por tanto, un valor numérico que está influido por el azar. Es decir que una variable aleatoria o estocástica es una función que asigna eventos (p.e. los resultados posibles de tirar o simplemente manipular las piedras azules; las piedras que engendran, (1,1), (1,2), (1,3)) a números reales (p.e. su suma). Una variable aleatoria o estocástica es una variable estadística que obtiene sus valores como resultado de mediciones hechas en experimento aleatorio. Al tener una variable aleatoria no podemos saber qué valor exacto tendrá; pero sí podemos asignarle una serie de valores posibles mediante una distribución de probabilidades, siempre y cuando se trate de una variable aleatoria discreta. Dicho de otro modo, los valores posibles para una variable aleatoria y sus valores probables asociados, establecen una distribución de probabilidad.
La definición formal de variable aleatoria se representa mediante esta fórmula:
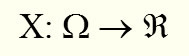
Donde X representa la función que asigna a cada elemento del espacio muestral (representado por omega) un número real (R). El conjunto de números reales está representado de esta manera por R.
Tenemos que enfrentarnos a la aleatoriedad infinita y podemos manejar esta aleatoriedad siempre y cuando no nos concentramos en patrones en el sentido de secuencias que son siempre exactas. Por tanto usaremos la estadística para encontrar de manera mucho más sutil un patrón llamado distribución de probabilidad discreta.
En este caso, nuestra variable aleatoria X = número de piedras producidas cuando se manipulan las piedras que generan.
Cada variable aleatoria debe seguir una distribución probable, la cual es una lista de todos los valores de X juntos con sus probabilidades.
A partir de la distribución de probabilidades podemos encontrar lo siguiente:
i. La media, y
ii. La varianza (es el cuadrado de la desviación estándar, y ésta es la medida de la dispersión de los datos que se emplean habitualmente)
La media = E [X] = suma [X*P(X)]
Var [X] = Var [X] =
Ejemplo: Supongamos que la piedra que engendra es manipulada ocho veces, como en el relato de Borges, y como producto de esa manipulación se va generando el siguiente número de piedras (además de la piedra azul original):
200, 7, 46, 82, 3, 102, 989, 21
i. Crear una distribución de probabilidad,
ii. Encontrar E [X] and Var [X]
Algunas veces, un fenómeno natural puede ser modelado para que encaje bien en un cierto tipo de distribución. Examinaremos tres clases de distribuciones aquí: binomial, de geometría, y de Poisson (llamada así en honor al físico-matemático francés Siméon-Denis Poisson (1781-1840)). Además de esto, haremos mínimas modificaciones a “Tigres azules”. Estas modificaciones nos permitirán examinar cada una de estas distribuciones.
Distribución Binomial
Consideremos una mínima modificación en el relato “Tigres azules”, donde cada vez que una piedra es manipulada, ocurre que otra piedra aparece o ninguna lo hace. Asumamos que una piedra aparece con probabilidad = p que no varía. Asumiendo que nosotros manipulamos las piedras un número fijo de veces y cada vez que lo hacemos es independiente de la siguiente vez.
En la modificación que hemos descrita, la variable aleatoria, X sigue una distribución binomial con parámetros “n” y “p”.
Podemos encontrar E [X] usando la fórmula n*p y Var [X] = n*p* (1-p)
Ejemplo: Asumiendo que tenemos la piedra azul de la historia de Borges que produce otra piedra con la probabilidad = .6 y no produce ninguna piedra con probabilidad = .4 Encontremos el número esperado de piedras si la piedra es manipulada ocho veces.
En este ejemplo n = 8, p = .6 entonces E [X] = n*p = 8*.6 = 4.8, Var [X] = n*p*(1-p) = 8*.6.4 = 1.96
Podríamos imaginar otro escenario con las piedras que generan donde la distribución binomial pueda ser usada en diez ensayos con el propósito de obtener una media = 6.
Distribución geométrica
Nuestra siguiente modificación involucra un escenario donde cada vez que las piedras azules son manipuladas, una nueva piedra azul aparece con probabilidad “p” o ninguna piedra aparece con probabilidad 1-p. En este escenario, sin embargo, X- número de manipulaciones hasta que la primera piedra aparezca, sigue una distribución geométrica, E [X] = 1/p, Var [X] = (1-p)/p2
Ejemplo, podríamos pensar también en otro escenario donde el número de piedras que aparece siga una distribución geométrica con una media = 5.
Distribución de Poisson
La modificación final que sugerimos implica un escenario donde otra vez, cada manipulación de las piedras resulta en ninguna piedra o en una piedra nueva. Sin embargo, no hay un número fijo de probabilidad “p” o un número fijo de manipulaciones. Asumimos que las piedras azules están siendo manipuladas siguiendo un índice constante sobre un intervalo dado de tiempo. Ahora X = número de piedras que aparecen sobre un intervalo de tiempo. X sigue la distribución de Poisson con una media y una varianza dadas = media.
Ejemplo, podemos pensar en una situación donde el número de piedras que aparecen en una hora si X sigue la distribución de Poisson con una media = 5/hora
Distribuciones continuas
Las distribuciones continuas son distribuciones donde la variable aleatoria X, puede tomar un número incontable o un número infinito de valores. Podemos también pensar en una situación donde las piedras que generan representen una variable aleatoria continua.
Puestos a reflexionar sobre el infinito nos imaginamos otra manera en la que podría haber actuado Cragie con las piedras azules. Una manera simple hubiera sido usar la distribución normal y crear un intervalo de confianza tal como sigue:
1.- Manipular la piedra un número fijo de veces = n
2.- Encontrar E [X] y una desviación estándar como describimos antes,
3.- Encontrar el intervalo apropiado “z” o intervalo.
Por lo expuesto anteriormente y de manera simplificada, hemos podido ver que la estadística bien puede aplicarse al realto “Tigres azules”. La estadística puede, en las manos de los personajes de Borges- que son arquetipos platónicos; se explican genéricamente- aliviar así su reacción aprehensiva al ser confrontados al devastador infinito.
El relato “Tigres azules” podría, desde luego, como lo hizo muy bien el estudioso Esteban Mata, ser analizado desde la perspectiva de la teoría del caos, y puede también ser comentado simplemente como un cuento fantástico donde suceden extraños fenómenos que no ameritan ni aceptan explicaciones racionales. También podríamos comentarlo en tanto un relato donde se plasma una fantasía metafísica, que de acuerdo a Bioy Casares, es la característica crucial de las fantasías borgeanas. Incluso podríamos analizar este cuento como si fuera una metáfora de la creación artística, específicamente del arte poética, o acaso como una contradicción entre la precisión y exactitud de las matemáticas y la imposibilidad de éstas de asimilar matemáticamente los sucesos que ocurren en el cuento. Nuestra lectura del cuento, ha privilegiado el sentido matemático, porque nos ha parecido que en efecto, “Tigres azules” es uno de los cuentos donde más abundan no solamente conceptos matemáticos, sino incluso términos matemáticos explícitamente empleados en el mismo relato. Nos ha parecido también que “Tigres azules” es uno de los relatos menos estudiados de Borges, especialmente desde la cantera de las matemáticas, disciplina que como bien sabemos, era una de las pasiones intelectuales de nuestro célebre autor Borges, tan erudito.
Hemos afirmado en un artículo anterior donde analizamos el poema “Descartes” y la visión de la geometría, el espacio y el tiempo que se deduce del poema y de otros textos borgeanos, que nada es casual en la obra de Borges. Tampoco es casual en absoluto que Borges hubiera decidido que el protagonista de “Tigres azules” fuera un profesor de lógica occidental, fascinado por los tigres y estudioso de Baruch Spinoza. ¿Qué explicación lógica podría haber dado Alexander Craigie a la transformación numérica sin orden ni concierto de las fabulosas piedras? Estamos de acuerdo con Jaime Alazraki, especialista en la obra de Borges, cuando afirma que el común denominador de las ficciones borgeanas sería un relativismo que influye y determina todo. Es claro que Borges nos presenta un universo en el que no podemos estar seguros de nada. En su relato “Tigres azules”, se refiere a la “aberración de las matemáticas”, -también llamado “obsceno milagro”- debido a la imposiblidad de entender la multiplicación y substracción inaudita de las piedras maravillosas que no parecen obedecer a ningún patrón conocido en el amplio ámbito de las leyes y fórmulas matemáticas. No es posible tan si quiera decir que 2 + 2 = 4 porque en el universo mágico de “Tigres azules”, precisamente esto no ocurre, más bien sucede todo lo contrario.
Utilizando la variable aleatoria discreta, concepto clave de la estadística, y además manipulando un poco la historia borgeana, hemos intendado presentar una posible explicación lógica a la realidad cambiante y cuantitativa presente en “Tigres azules”. Nuestra intención, como hemos mencionado, ha sido sobre todo la de hacer más manejable para los estudiantes universitarios, algunos conceptos matemáticos de la estadística, al pensar en ejemplos concretos provenientes de relatos, como en este caso, que además permitan a los estudiantes ampliar sus horizontes académicos al leer buena literatura. Comentaremos luego, la relación que hemos encontrado entre los dos cuentos analizados en cuanto a la visión del mundo que Borges nos presenta en ellos.
En el relato “El espejo y la máscara”, el poeta de la corte representaría a todos los poetas, y de esta manera, desde luego, al mejor usuario del lenguaje. Es muy interesante que justamente el experto en las palabras no sea capaz de entender todo el lenguaje, de transmitir a través de su arte la realidad o su visión de la misma, de expresar la Belleza o la Verdad mediante ella. En “Tigres azules”, también el profesor Craigie es experto en lógica occidental y sin embargo no será capaz de entender la lógica de la transformación numérica de las piedras azules.
En “El espejo y la máscara”, el Rey del cuento le regala al Ollán un espejo como premio por su primer poema que era una mímesis de la realidad. El poeta ha intentado reflejar la realidad y de esta manera estaría funcionando no en el universo regido por la “episteme”, sino en el ámbito de la “doxa”, de las apariencias, porque la descripción fotográfica de la realidad no la agota ni la representa en su totalidad. El segundo regalo del Rey de Irlanda fue una máscara de oro y correspondía al segundo poema que escondía la realidad; ya no era una descripción puntillosa de la batalla como en el primer poema, sino más bien “era la misma batalla”. El poeta tuvo que librar su batalla personal con el lenguaje al escribir el segundo poema que ya no era un calco de la realidad. El tercer poema del Ollán siendo el más breve de todos, y también el más intenso, representa la maravilla de todas las maravillas, el absoluto estético. De alguna manera podemos decir que el poeta ha destruído el lenguaje al trascenderlo. El poeta ha roto el lenguaje al acceder a la maravilla con una sola palabra o tal vez una breve frase esencial. El Rey y el poeta pagarán por esa “hamartía”; el Rey por ser testigo de lo imposible, por haber instigado la maravilla, y el poeta por haberla ejecutado aplicadamente, y por tanto, por haber actuado como si fuera Dios, tal como Alexander Craigie lo hiciera en “Tigres azules”.
El lenguaje es lineal y la realidad es simultánea, y por ende, el poeta del relato “El espejo y la máscara” no puede aunque lo intenta aprehender la realidad mediante el lenguaje, no obstante ser pues, en tanto poeta, el mejor usuario del lenguaje. El poeta tampoco puede acceder a la Belleza mediante el lenguaje humano, y la Belleza con mayúscula, como aparece en el relato de Borges, puede de hecho ser un sinónimo de la Verdad en este relato plurisignificativo. Al salir del palacio, el poeta se suicida con la daga regalada por su Rey. Por su parte, el Rey de Irlanda dejó de ser rey para ser un vagabundo que no repitió nunca el misterioso poema-línea o acaso poema-palabra que sin embargo encerraba la Maravilla y la Belleza.
En ambos cuentos ocurren “hamartías” muy importantes y similares. Alexander Craigie, manipula unas piedras sagradas que se multiplican y disipan de manera inexplicable para los seres humanos. Su inefable acción es un desafío muy caro que pone en evidencia la limitación de las matemáticas para explicar transformaciones numéricas. El poeta de la corte impelido por su rey se atreve a quebrar el lenguaje al intentar acceder a la Belleza = Verdad por medio de las palabras. Alexander Craigie casi se vuelve loco intentado entender lo incomprensible, y se salva de la locura al entregar las piedras azules a cambio de la normalidad en su vida : “ […] Te quedas con los días y las noches, con la cordura, con los hábitos, con el mundo.”
Borges nos presenta en ambos relatos una visión del mundo impregnada de relativismo. Como bien señala Alazraki, el relativismo característico de los relatos borgeanos nos incita a ver el mundo en continuo movimiento, nos invita a tratar de trasdender el “hic et nunc”, a buscar todas las dimensiones posibles de la realidad. Para Borges, el mundo es impenetrable, y el universo es incomprensible para los seres humanos, y por tanto, cualquier intento por descrifrar el universo conducirá al fracaso. En el caso del poeta del relato “El espejo y la máscara”, su “hamartia” le condujo al suicidio, y al rey lo redujo a la condición de paria. En el cuento “Tigres azules”, la “hamartía” de Alexander Craigie lo alienó y fue rescatado de esa alienación tras rogar a Alá que su vida volviera a la normalidad. Solamente es salvado cuando le entrega las piedras mágicas o diabólicas al misterioso mendigo ciego que se las pidió a cambio de devolverle la cordura y el mundo.
Como bien señala Alazraki en La prosa narrativa de Jorge Luis Borges (1974),
“ Borges ha negado la validez de la metafísica en el contexto
de la realidad, pero la ha aplicado a un contexto donde
recobra su vigencia: la literatura.”
Concluimos afirmando que para efecto de nuestro colectivo de aprendizaje, los textos matemáticos de Borges son muy útiles para incitar a que los estudiantes piensen de manera crítica, a que amplíen sus conocimientos literarios a la misma vez que sus estudios de estadística dan un giro de muchos grados al trabajar con ejemplos que nunca hubieran imaginado. Las humanidades y las ciencias se abrazan en armonía gracias a los múltiples y eruditos conocimientos de Borges. Los estudiantes en nuestro colectivo de aprendizaje se enriquecerán no sólo académicamente sino también desde una perspectiva más global y humana.
De hecho, Borges nos maravilla y nos transforma; nos impele a cuestionarnos a cada paso, a reflexionar sobre el mundo, a dudar de lo que creemos seguro, a mirar la realidad con ojos de poeta y de filósofo. ¿Quién se atrevería a decir que sigue siendo la misma persona después de leer un texto de Borges?
* * *
Bibliografía Consultada
Alazraki, J.: Versiones-inversiones-reversiones, Madrid, Gredos, 1977.
Alazraki, J.: Jorge Luis Borges, Nueva York: Columbia University Press, 1971.
Balderston, Daniel. “The Theory of Games and Genetic Criticism: On the Manuscript of ‘La Lotería en Babilonia’,” Variaciones Borges, 36 (2003). 155-165
Barrenechea, A.M.: La expresión de la irrealidad en la obra de J.L.Borges, México: El Colegio de México, 1957.
Borges, Jorge Luis, Obras Completas. Buenos Aires, EMECE. 1996.
Kcenich, Stephen; Bosse, Michael J. “$158 per Quart: The Value of a Volume of Coins,”
AMATYC Review, v29 n2 p15-21 Spr. 2008.
Kcenich, Stephen; Bosse, Michael J. “Extending Rules for Exponents and Roots Utilizing Mathematical Connections.” AMATYC Review, v27 n2 p19-29 Spr 2006.
Luna-Escudero-Alie, María-Elvira. “Reflexiones sobre los límites del lenguaje en ‘El espejo y la máscara’ de Jorge Luis Borges”. Espéculo, Revista de estudios literarios. Universidad Complutense de Madrid, 22 (2002),
http://www.ucm.es/info/especulo/numero22/espejo.html
Mata, Esteban. “Los azules tigres del caos, un vistazo al pensamiento de la complejidad en la obra de Jorge Luis Borges.” Rev. Filosofía Univ. Costa Rica, XLVII (120-121), (2009). 37-44.
Mateos, Zulma. Filosofía en la obra de Jorge Luis Borges, Buenos Aires, Biblos, 1998.
Rodríguez Monegal, E.: Borges par lui-même, París: Ed.du Seuil, 1970.